The Dark Art of Estimating Flood Risks

The 100-year flood and the 500-year flood are both very rough estimates.

My title is a little unfair. So far as I can tell, the people who are trying to figure out the 100-year or 500-year floods in various places are hard-working professionals, applying their expertise to a difficult problem. But there are a lot of uncertainties that get concealed behind the final numbers. The consequence is that the estimates can be way off. For instance, a 2012 study of Houston found that over 47% of all flood insurance claims were located outside of the designated 100-year floodplain boundary.

From what I’ve been able to learn so far, here are some of the key uncertainties, starting with the most widely discussed:

Climate change. The estimates are based on historic experience, assuming that flood risks are stable over time. Climate change is going to increase the likelihood of floods in many areas, so the estimates are biased downward. But it’s not easy to know how much to adjust, because the climate models can’t give precise forecasts of the amount of change in any given locale.

Hydrological changes. Flood risks can also change because of changes in land use. One big problem in Houston has been the destruction of important natural sinks that help control flooding. Impervious surfaces also increase flood risks, because water is released more quickly. Land subsidence can also increase flood risk. Adjusting for these factors has to be complicated — and there can also be uncertainties because we can’t precisely forecast future urban development.

Limited data. For inland flooding, flood estimates are based on hydrological gauges in streams. (Hurricanes, on the other hand, are fairly rare events, so the data base for them is inherently limited.) There may be a limited number of gauges in some areas, or they may not have been in operation very long. Also, gauges may be inaccurate, particularly in periods of high flow. Efforts are made to adjust for some of these issues, for example with comparisons to gauges in nearby areas. But this involves judgment calls.

Poorly known probability distributions. We don’t have a theoretical basis for predicting how river flows vary over time. The government did a study and found that, of the standard distributions used by statisticians, something called the Pearson Type III distribution with log transformation worked the best for fitting the data on high stream flows (i.e., floods). (Don’t feel bad if you don’t know what that is; I had to look it up. Basically, it’s a normal “bell curve” that has been stretched in one direction or “skewed.”) But this is an approximation., since in fact we don’t know the true shape of the probability distribution. So the statistical method being used is only approximately right to begin with.

The difficulty of estimating rare events. By definition, increasingly rare events are increasingly unlikely to be found in the record of the time period for which we have data. That means that there’s going to be a lot of uncertainty about high-end estimates, which involve rare events like 500-year floods. For example, in a situation studied by the National Research Council in 2000 (see this report at p. 81). , the expected discharge for the 100-year flood (p = 0.01) is 4,310 cubic feet of water per second (cfs), the upper confidence limit is 6,176 cfs, and the lower limit is 3,008 cfs. So basically, what we know is that there’s a 90% chance that the 100-year flood would involve somewhere between 3008 cfs and 6,176 cfs, a difference of a factor of two. By 2000, the Army Corps of Engineers had already decided that it needed to start taking this uncertainty into account, but I wonder how many other flood control agencies and land use planners are that sophisticated?

By pointing out these issues, I certainly don’t mean that we should ignore the estimates that come out of this process. I certainly don’t have enough expertise to criticize these methods, though it does bother me somewhat that the methodology hasn’t been changed since 1982. But even if the 1982 guidance is still state of the art, we need to realize that what we’re getting is a “best professional judgment,” not a scientifically precise number.

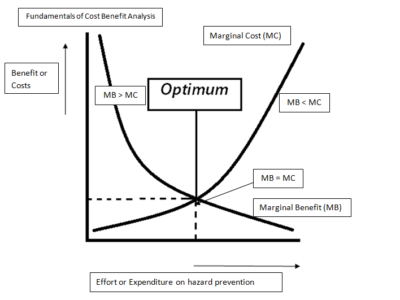
When thinking about policy, it’s really important to include sensitivity analysis to take into account these uncertainties. We also have to keep in mind that factors 1 and 2, at least, lead to systematic underestimates of risk. That’s a good reason to add a significant margin of safety, or put differently, to take a precautionary approach to managing flood risks. Neither policy analysis nor engineering are exact sciences. That’s why we need policies and designs that are robust enough to work even if our numbers are a bit off.

One Reply to “The Dark Art of Estimating Flood Risks”

Thanks for this post!

At least three other things to keep in mind:

1) The “100-year flood” and “500-year-flood” are poorly named, and are increasingly being called, more accurately, a 1% chance annual flood and a 0.2% chance annual flood. This is important because people tend to think if a 100-year flood came recently, it can’t come again very soon. But floods are not like earthquakes – there’s no built up tension that gets released. If there was a 100-year flood last year, there’s still a 1% chance of another 100-year flood this year. In New England, where we work, for example, we had three 100-plus-year, regional-scale floods, in 11 years – 1927, 1936 and 1938.

2) In many geographical areas, there is enough natural diversity that somewhere within a given region there is a large flood every year. In New England, there is a 100-year flood somewhere in the region essentially every year.

1) and 2) together mean that we need to understand large floods as common and frequent events, regardless of the specifics of the technicalities of what we consider a 1% annual chance flood (though as you point out those specifics and technicalities matter enormously).

3) Floods carry more than water; they also carry sediment and debris. Also, they are not just rising water but moving water. Especially if there’s any slope involved, this means they can have tremendous force, and as a result, they don’t just cover the land; they tear up chunks of landscape and infrastructure and move it. Even in low-slope environments, floods carry considerable amounts of sediment and can cause major landscape changes. The problem with this in terms of flood prediction is that many infrastructure, emergency response and other related guidelines are based only on hydraulic standards, i.e. the _water_ expected in a 50-year, 100-year, etc. flood, and are still inadequate, even if the predictions for chance of a flood are relatively accurate. Predictions of flood need to include not just water volume predictions but predictions about sediment, debris, and force; and standards and guidelines need to be set accordingly.

For those who are interested, these basic ideas are covered in a very reader-friendly fashion in a report we published last year: https://extension.umass.edu/riversmart/policy-report. Though focused on New England the principles apply more widely.

Comments are closed.

Reader Comments

Eve Vogel says:

September 1, 2017 at 6:34 am

Thanks for this post!

At least three other things to keep in mind:

1) The “100-year flood” and “500-year-flood” are poorly named, and are increasingly being called, more accurately, a 1% chance annual flood and a 0.2% chance annual flood. This is important because people tend to think if a 100-year flood came recently, it can’t come again very soon. But floods are not like earthquakes – there’s no built up tension that gets released. If there was a 100-year flood last year, there’s still a 1% chance of another 100-year flood this year. In New England, where we work, for example, we had three 100-plus-year, regional-scale floods, in 11 years – 1927, 1936 and 1938.

2) In many geographical areas, there is enough natural diversity that somewhere within a given region there is a large flood every year. In New England, there is a 100-year flood somewhere in the region essentially every year.

1) and 2) together mean that we need to understand large floods as common and frequent events, regardless of the specifics of the technicalities of what we consider a 1% annual chance flood (though as you point out those specifics and technicalities matter enormously).

3) Floods carry more than water; they also carry sediment and debris. Also, they are not just rising water but moving water. Especially if there’s any slope involved, this means they can have tremendous force, and as a result, they don’t just cover the land; they tear up chunks of landscape and infrastructure and move it. Even in low-slope environments, floods carry considerable amounts of sediment and can cause major landscape changes. The problem with this in terms of flood prediction is that many infrastructure, emergency response and other related guidelines are based only on hydraulic standards, i.e. the _water_ expected in a 50-year, 100-year, etc. flood, and are still inadequate, even if the predictions for chance of a flood are relatively accurate. Predictions of flood need to include not just water volume predictions but predictions about sediment, debris, and force; and standards and guidelines need to be set accordingly.

For those who are interested, these basic ideas are covered in a very reader-friendly fashion in a report we published last year: https://extension.umass.edu/riversmart/policy-report. Though focused on New England the principles apply more widely.